머신러닝을 위한 선형대수, 벡터, 행렬 연산

🟫 선형대수

◾ 선형 대수학은 데이터의 수학이다.

◾ 선형 대수학은 통계 분야에 많은 영향을 끼쳤다.

◾ 선형 대수학은 푸리에 급수 및 컴퓨터 그래픽과 같은 여러 분야에서 수학적인 도구의 기초가 된다.

◾ 스칼라는 어떤 것을 표현하는 값이다.

 

🟫 벡터(Vectors)

◾ 컴퓨터 과학자들은 벡터를 무언가는 나타내는 숫자 목록으로 해석할 수 있다.

◾ 물리학자들은 벡터를 방향이 있는 스칼라로 간주하며 평면과 무관하다고 간주한다.

◾ 수학자들은 벡터를 두 가지의 조합으로 간주하고 이를 일반화 시키려고 노력한다.

◾ 선형 대수는 벡터 연산이 많은 부분을 차지하고 있으며 벡터는 스칼라라고 하는 하나 이상의 값으로 구성된 튜플이다.

🟤 벡터 연산

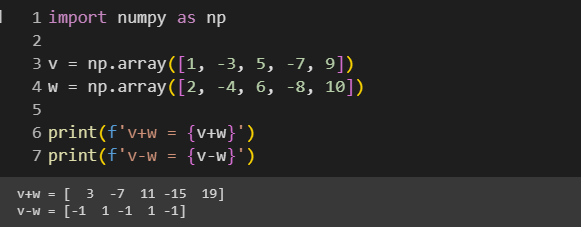
  ◾ 벡터 덧셈(vector addition)과 뺄셈(vector subtraction)

 ◾ 스칼라 곱셈

벡터를 스칼라와 곱셈을 수행하면 그 값이 거지거나 줄어든다. 이는 벡터에 양수나 음수를 곱하는 행위에 따라 결정된다.

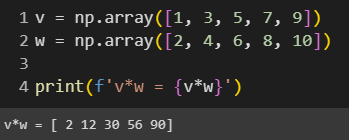
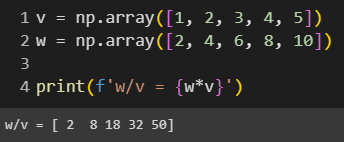
 ◾ 벡터 곱셈, 나눗셈

덧셈과 뺄셈 연산과 마찬가지로 곱셈, 나눗셈 연산도 요소를 기반으로 수행되며 같은 길이의 새로운 벡터가 생성된다.

 

◾ 벡터의 길이와 내적(vector length and dot product)

• 길이가 같은 두 벡터를 곱한 요소들의 합을 계산하게 되면 스칼라값을 얻을 수 있다. 이는 연산을 위해 사용되는 내적 연산자 때문에 이를 내적이라고 한다.
• 내적은 벡터 투영, 벡터 분해를 계산하고 직교성을 결정하기 위해 많이 사용된다.
• 내적 연산은 머신러닝에서 벡터의 가중치 합을 계산하는 데 사용된다.

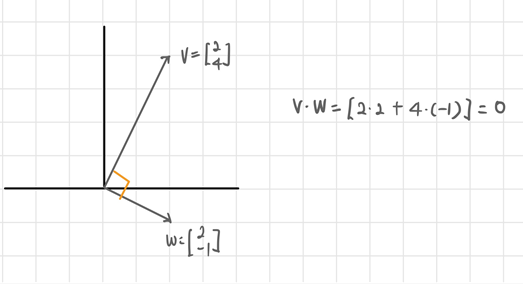
수학에서는 0은 항상 특2별한 의미를 갖는다.

내적의 경우에는 두 벡터가 수직(perpendicular)임을 의미한다.

 

 

 

 

 

 

 

벡터의 길이 공식 및 파이썬 구현

🟫 벡터 노름(Vector Norms)

어떤 벡터를 길이나 크기와 같은 양적인 수치를 계산하기 위해서 직접 계산하거나 벡터 연산 또는 벡터-행렬 연산을 이용할 수 있다. 벡터의 길이는 벡터 노름 또는 벡터의 크기라고 한다. 벡터의 길이는 공간에서 벡터의 범위를 나타내는 음이 아닌 수자이며 이를 벡터의 크기 또는 노름이라고 한다.

 

🟫 행렬 연산(Matrix Operation)

행렬의 사칙연산은 각각의 요소별로 이루어진다.

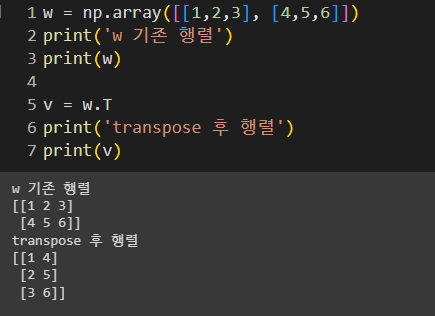
◾ 전치(transpose)행렬 : 행렬의 행과 열을 교환하는것

 

🟫  고유 분해(Eigendecomposition)

• 행렬 분해는 복잡한 연산의 범위를 단수화하기 위해 행렬을 부분으로 줄이는 유용한 도구
• 가장 많이 사용되는 행렬 분해 유형은 고유벡터와 고유 분해
• 이는 주성분 분석(Principal Component Analysis)과 같은 머신러닝에서도 중요한 역할을 한다.
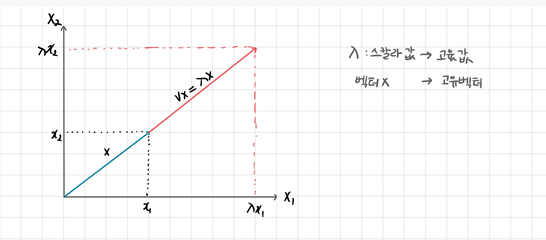
• 고유벡터는 길이 또는 크기가 1인 단위 벡터이다. 이는 오른쪽 벡터라고 불리며, 횡 벡터라 부르는 왼쪽 벡터와 반대인 열벡터를 의미한다.
• 고윳값은 벡터에 길이 또는 크기를 제공하는 고유벡터에 적용되는 계수이다.

파이썬으로 구현